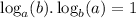Question

Show that for any positive numbers a and b with a ≠ 1 and b ≠ 1, loga(b) ∙ logb(a) = 1.

Answer 1

logₓ(y) =
`(\log(y))/(\log(x))`

`(\log(b))/(\log(a))*(\log(a))/(\log(b))`

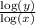
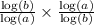
or

= 1

Explanation:

Data provided:

a ≠ 1 and b ≠ 1

To prove
`\log_a(b).\log_b(a)=1`

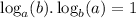
RHS = 1

LHS =
`\log_a(b).\log_b(a)`

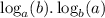
Now,

We have the property of the log function as:

logₓ(y) =
`(\log(y))/(\log(x))`

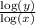
applying the above property on the LHS side to solve LHS, we get

LHS =
`(\log(b))/(\log(a))*(\log(a))/(\log(b))`

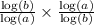
or

LHS = 1

Since,

LHS = 1 is equal to the RHS = 1

Hence, proved that
`\log_a(b).\log_b(a)=1`