Question

A silver wire 2.6 mm in diameter transfers a charge of 420 Cin 80 min. Silver contains 5.8 \times 10^{28} free electrons per cubic meter.What is the current in the wire?What is the magnitude of the drift velocity of the electronsin the wire?

Answer 1

The current in the wire is 0.0875 A and the drift velocity of the electrons in the wire is 1.77x10^{-6} m/s.

Step-by-step explanation:

Facts that you know from the problem statement:

Using the diameter of the wire the radius is r=d/2. r=2.6/2= 1.3 mm. It is useful to have the time in seconds so t=80 min = 4800 s. You know the charge Q= 420 C. The concentration of electrons in the wire is n = 5.8*10^{28}.

The current in the wire is the net charge that flows through the area in a second, the units are amperes (A), and it is given by:

`I=(Q)/(t)`

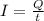
Replace the values:

`I=(420C)/(4800s)=0.0875 A`

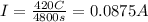
The drift velocity in the electrons in the wire (V) is given by the equation:

`V=(I)/(n|q|(pi)r^2)`

Replace the values that you have and the charge of an electron taht is equal to 1.6*10^{-19}

`V=(0.0875)/((5.8*10^(28))(1.6*10^(-19))0.0013^2(pi))`

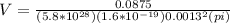
V=1.77x10^{-6} m/s