Answer:
x = -4 , 4
Explanation:
The point (x,4) is equidistant from (0,1) and line y=-1
y=-1, it is horizontal line.
Let point on line be (x,-1)
Distance formula:

Distance between (x,4) and (x,-1) = Distance between (x,4) and (0,1)
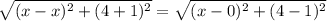
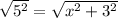
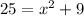

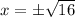
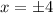
hence, the value of x is 4 and -4