Question

Use logarithmic properties and the fact that ln(2) ≈ 0.69 and ln(3) ≈ 1.10 to approximate the value of each of the

following logarithmic expressions. Do not use a calculator.
ln(8/3)

Answer 1

The answer is 0.97

Explanation:

Hi, we need to use the log properties taking into account that Ln(2) is aprox. 0.69 and Ln(3) is aprox. 1.10. I think you can understand better as we solve it, so here it goes.

`Ln((8)/(3) )=Ln(8)-Ln(3)`

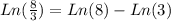
Since:

`8=2^(3)`

`Ln(2^(3) )-Ln(3)`

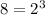
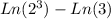
Then

`3Ln(2)-Ln(3)`

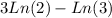
Now, we have everything where we want it, in terms of Ln(2) and Ln(3), now it is easy to solve.

`3(0.69)-1.10`

`2.07-1.10=0.97`

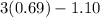
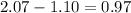
Best of luck.