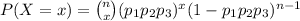Answer:
The probability is:
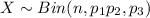
or
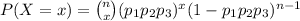
Explanation:
Consider the provided information.
Each of the n people will register with probability p1. Given that a person registers, he or she will vote with probability p2. Given that a person votes, he or she will vote for Kodos (who is one of the candidates) with probability p3.
There is only one way to vote for Kodos
That is the person should be register, and will vote in the favor of Kodos.
Hence, the probability is:
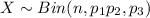
Where X is the number of votes for Kodos.
The Required PMF is: