Question

By finding the radius of each circle and the distance between their centers, show that the circles x²+y²=4 and x²-4x+y²-4y+4=0 intersect. Illustrate graphically.

Answer 1

The circles do intersect.

Explanation:

A circle is of the form

(x-h)^2+(y-k)^2=r^2

where,

h = Point on x axis of the circle center

k = Point on y axis of the circle center

`x^2+y^2=4\\\Rightarrow (x-0)^2+(y-0)^2=2^2`

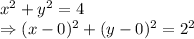
So, the center of the circle is at (0,0) and radius is 2 units

`x^2-4x+y^2-4y+4=0\\\Rightarrow (x^2-4x)+(y^2-4y)=-4\\\Rightarrow (x-2)^2+(y-4)^2=-4\\\Rightarrow (x^2+4-4x)+(y^2+4-2y)=-4\\\Rightarrow (x-2)^2+(y-2)^2=-4+4+4\\\Rightarrow (x-2)^2+(y-2)^2=4\\\Rightarrow (x-2)^2+(y-2)^2=2^2`

The circle center is at the point (2,2) and radius is 2 units.

Hence, the circles do intersect.