Question

consider the followin polynomials equations a=3x2(x-1) b= -3x3+4x2-2x+1 . perform each operation and determine if the result is a polynomial. is the result of a+b a polynomial? is the result of a-b a polynomial? is the result of a*b a polynomial?

Answer 1

All three operations lead to polynomials.

See explanations below.

Explanation:

Polynomial a =
`3x^2(x-1)=3x^3-3x^2`

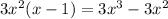
Polynomial b =
`-3x^3+4x^2-2x+1`

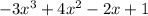
Therefore:

a + b =
`3x^3-3x^2+(-3x^3+4x^2-2x+1)=\\=3x^3-3x^2-3x^3+4x^2-2x+1=\\=x^2-2x+1`

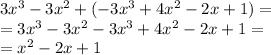
where we have combined all like terms. This is clearly another polynomial (of grade 2)

a - b (here we need to flip all signs inside the parenthesis when we remove this grouping symbol):
`3x^3-3x^2-(-3x^3+4x^2-2x+1)=\\3x^3-3x^2+3x^3-4x^2+2x-1=\\6x^3-7x^2+2x-1`

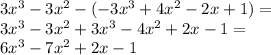
which is clearly another polynomial (but of grade 3)

a * b : (here we use distributive property to multiply each term of the first polynomial by each term of the second one, and then combine like terms)

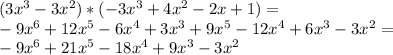`(3x^3-3x^2)*(-3x^3+4x^2-2x+1)=\\-9x^6+12x^5-6x^4+3x^3+9x^5-12x^4+6x^3-3x^2=\\-9x^6+21x^5-18x^4+9x^3-3x^2` which is indeed another polynomial (this time of grade 6)