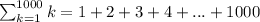Answer:
Explanation:
You have to use the summation notation formula:
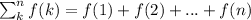
where k is the starting number, n is the ending number and f(k) is the function or the expression to be added.
In this case, you have the sum of the integer numbers from 1 to 1000. Therefore, k=1 and n=1000.
Now, you have to obtain the function f(k) which is the representation of the expression needed to obtain the correct result of the sum.
f(k=1) = 1
f(k=2)=2
f(k=3)=3 ...
You can notice that the value of k corresponds to te value of f(k) therefore f(k) = k
Replacing the values of k, n and f(k) in the formula: