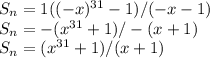Question

Use the geometric series formulas to find the sum of the geometric series.

1 − x + x2 − x3 + ⋯ + x30 in terms of x

Answer 1

The sum of the geometric progression is
`S_n=(x^(31)+1)/(x+1)`.

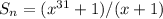Explanation:

Given data in the question:-

`1-x+x^2-x^3+x^4+........+x^(30)`

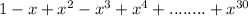
We have to find the sum of Geometric Progression.

Solution:-

As we know the sum of geometric progression is

`S_n=a(r^n-1)/r-1\\`

Where r is the common ratio defined as
`r=T_n/T_(n-1)`

`r=-x/1`

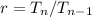
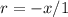
n(no of terms)=31

`S_n=1((-x)^(31)-1)/(-x-1)\\S_n=-(x^(31)+1)/-(x+1)\\S_n=(x^(31)+1)/(x+1)`