Answer
given,
A =
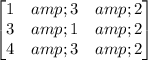
B =
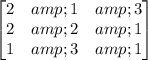
a) C = A + B
C =

C =
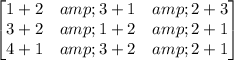
C =
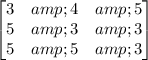
the resulting matrix represent the cities and the route in a single matrix of both the company together.
C₁ ₃ = means city 1 have routes
so, C₁ ₃ = 5
b) D = B + A
D =

D =
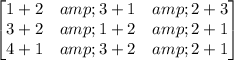
D =
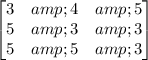
D₁ ₃ = means the value of the element on the first row and third column
so, D₁ ₃ = 5
c) both the matrix represent same value
we can say that matrix addition follows commutative law
A + B = B + C