Answer:
The sum is 493.4
Explanation:
In order to find the value of the sum, you have to apply the geometric series formula, which is:
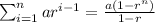
where i is the starting point, n is the number of terms, a is the first term and r is the common ratio.
The finite geometric series converges to the expression in the right side of the equation. Therefore, you don't need to calculate all the terms. You can use the expression directly.
In this case:
a=40
b= 1.005
n=12 (because the first term is 40 and the last term is 40(1.005)^11 )
Replacing in the formula:
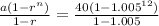
Solving it:
The sum is 493.4