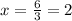Question

Solve each system of equations by writing a new system that eliminates one of the variables.

3x+2y=4
4x+7y=1

Answer 1

`x=2\\y=-1`

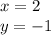
Explanation:

Let:

`3x+2y=4\hspace{5}(1)\\and\\4x+7y=1\hspace{5}(2)`

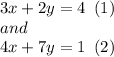
We need to eliminate one of the variables, so let's use elimination method. First multiply (1) by 4 and (2) by 3:

`4*(1)\equiv\hspace{5}12x+8y=16\\3*(2)\equiv\hspace{5}12y+21y=3`

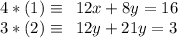
Now subtract 3*(2) from 4*(1) in order to eliminate x:

`4*(1)-3*(2)\\12x-12x+8y-21y=16-3\\-13y=13`

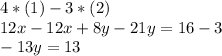
Solving for y:

Multiplying both sides by -1/13

`y=-(13)/(13) =-1`

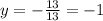
Finally, replacing the value of y in (1)

`3x+2*(-1)=4`

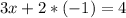
Solving for x:

add 2 to both sides:

`3x=6`

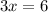
Multiply both sides by 1/3:

`x=(6)/(3) =2`