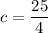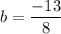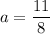Answer:
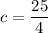
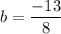
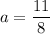
Explanation:
given ,
equation y=ax²+bx+c
passing through points (1,6), (3, 20), and (−2,15).
then these points will satisfy the equation
at (1,6)
y = a x²+b x+c
6 = a(1)² + b (1) + c
a + b + c = 6------(1)
at (3 , 20)
y = a x²+b x+c
20 = a(3)² + b (3) + c
9 a + 3 b + c = 20------(2)
at (−2,15)
y = a x²+b x+c
15 = a(-2)² + b (-2) + c
4 a -2 b + c = 15------(3)
solving equation (1),(2) and (3)
a = 6 - b - c
9 (6 - b - c)+ 3 b + c = 20
6 b + 7 c = 34-------(4)
4 (6 - b - c) -2 b + c = 15
2 b + c = 3----------(5)
on solving equation (4) and (5)