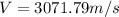Answer: 3071.79 m/s
Step-by-step explanation:
Approaching satellite's orbit around the Earth to a circular orbit, we can use the equation of velocity in the case of uniform circular motion:
 (1)
(1)
Where:
 is the velocity of the satellite
is the velocity of the satellite
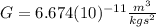 is the Gravitational Constant
is the Gravitational Constant
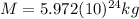 is the mass of the Earth
is the mass of the Earth
 is the radius of the orbit
is the radius of the orbit
Now, if we want the satellite to move in a geosynchronous orbit, it needs to travel at a specific orbiting radius and period to fulfill this condition. This means the satellite's orbital period
 must match Earth's rotation on its axis, which takes one sidereal day ( approximately 24 h).
must match Earth's rotation on its axis, which takes one sidereal day ( approximately 24 h).
So, if the satellite travels one complete circle
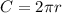 in a period
in a period
 , its velocity is also expressed as:
, its velocity is also expressed as:
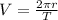 (2)
(2)
Where
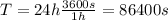
Combining (1) and (2):
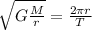 (3)
(3)
Isolating
 :
:
![r=\sqrt[3]{x(GMT^(2))/(4 \pi^(2))}](https://img.qammunity.org/2020/formulas/physics/high-school/zse19oxxdgts7azgvdxj2kpg9t4ilxj5c5.png) (4)
(4)
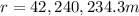 (5)
(5)
Substituting (5) in (1):
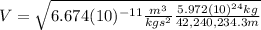 (6)
(6)
Finally: