Answer: 7546.76 years
Step-by-step explanation:
This can be solved by the following equation:
 (1)
(1)
Where:
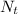 is the number of atoms of carbon-14 left after time
is the number of atoms of carbon-14 left after time

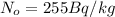 is the defined atmospheric carbon-14 (the number of atoms of C-14 in the original sample)
is the defined atmospheric carbon-14 (the number of atoms of C-14 in the original sample)
 is the rate constant for carbon-14 radioactive decay
is the rate constant for carbon-14 radioactive decay
 is the time elapsed
is the time elapsed
On the other hand,
 has a relation with the half life
has a relation with the half life
 of the C-14, which is
of the C-14, which is
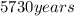 :
:
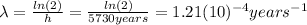 (2)
(2)
In addition, we can calculate the value of
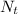 knowing the mass
knowing the mass
 of the sample and the decay rate
of the sample and the decay rate
 :
:

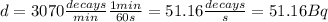
Then:
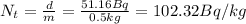 (3)
(3)
Now, we have to find the age of the sample
 from (1):
from (1):
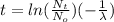 (4)
(4)
Substituting (2) and (3) in (4):
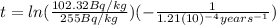 (4)
(4)
Finally:
 This is the age of the sample
This is the age of the sample