Question

Solve the following exponential equations.
10^(3x−5) = 7^x

Answer 1

x = 2.3202

Explanation:

Given equation:

`10^((3x-5)) = 7^x`

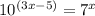
on taking log both sides, we get

`\log(10^((3x-5))) =\log(7^x)`

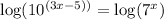
now,

using the property of log function

log(aᵇ) = b × log(a)

therefore,

we get

(3x-5)log(10) = xlog(7)

now,

log(10) = 1

and

log(7) = 0.84509

thus,

( 3x - 5 ) × 1 = 0.84509x

or

3x - 0.84509x - 5 = 0

or

2.15491x = 5

or

x = 2.3202