Question

Use the properties of logarithms to rewrite each expression in an equivalent form containing a single logarithm.

log (5/6 )− log (2/3)

Answer 1

log(5/4)

Explanation:

You have to apply the properties of logarithms to the given expression in order to obtain a form with a single logarithm.

For example, the quotient rule:

`log((x)/(y)) = log(x) - log (y)`

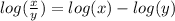
In this case, log(x) = log (5/6 ) and log(y)= log (2/3)

Therefore x = 5/6 and y = 2/3

Applying the rule:

log (5/6 )− log (2/3) =
`log((5/6)/(2/3))`

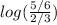
Solving the argument of the logarithm (The division of the fractions)

`(5/6)/(2/3) = ((5)(3))/((6)(2)) =(15)/(12) =(5)/(4)`

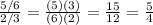
The equivalent form is:

log(5/4)