Question

Does there exist a pair of consecutive even integers whose reciprocals sum to 3/4? Explain how you know.

Answer 1

2, 4

Explanation:

Let there are two unknown consecutive pairs of even integers 2n and 2n+2.

If the sum of the reciprocals of those two integers is 3/4, then we can write,

1/2n +1/(2n+2) =3/4 ...... (1)

Solving this above equation we can check whether the integers exist or not.

Now, from equation (1) we get,

1/n +1/(n+1) =3/2

⇒
`2(2n+1)=3n(n+1)`

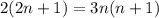
⇒4n +2 =3n²+3n

⇒3n²-n-2 =0

⇒ (n-1)(3n+2) =0

⇒ (n-1) =0 {Since if (3n+2) =0 then, n will be a negative fraction, which is not possible}

⇒ n=1

∴ 2n =2 and 2n+2 =4

Hence, the two integers are 2, 4. (Answer)