Question

Solve the following equation. Remember to check for extraneous solutions 7/(b+3) + 5/(b-3) = (10b-2)/(b²-9).

Answer 1

b= 2 is the solution for the given equation.

Explanation:

Here, the given expression is:

`(7)/((b+3))  + (5)/((b-3)) = (10b -2)/((b^(2) -9))`

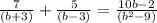
Simplifying Left side, we get

`(7)/((b+3))  + (5)/((b-3))`

=
`(7(b-3) + 5(b+3))/((b+3)(b-3))`

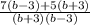
Also, by ALGEBARIC IDENTITY:
`x^(2) -y^(2) = (x+y)(x-y)`

So,
`(b+3)(b-3) = b^(2) -9`

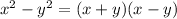
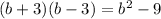
So, LHS becomes
`(7(b-3) + 5(b+3))/(b^(2) -9)`

Compare both Left side, Right side we get

`(7(b-3) + 5(b+3))/(b^(2) -9)` =
`(10b -2)/((b^(2) -9))`

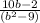
or, 7(b-3) + 5(b+3) = 10b -2

⇒ 7b - 21 + 5b + 15 = 10b -2

or, 12b - 10b = 6-2

or, 2b = 4 ⇒ b = 4/2 = 2

⇒ b= 2 is the solution for the given equation.