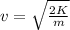Question

If a golf ball and a ping-pong ball both move with the same kinetic energy, can you say which has the greater speed? Explain in terms of KE. Similarly, in a gaseous mixture of massive molecules and light molecules with the same average KE, can you say which has the greater speed?

Answer 1

The ping pong ball, the light molecules have greater speed

Step-by-step explanation:

The kinetic energy of an object is defined as

`K=(1)/(2)mv^2`

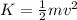
where

m is the mass of the object

v is its speed

It follows that the speed can be written as

`v=\sqrt{(2K)/(m)}`

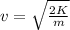
In this problem, both the golf ball and the ping pong ball have kinetic energy K. However, the mass of a gold ball is larger (approx. 45 g) than that of a ping pong ball (approx. 4 g): therefore, since v is inversely proportional to the square root of the mass, it follows that the ping pong ball must have a greater speed in order to achieve the same kinetic energy of the golf ball.

The same argument can be applied to the gaseous mixture: if there are more massive molecules and light molecules, and if they all have the same kinetic energy, then this means that the light molecules must have a greater speed, as a result again of the equation

`v=\sqrt{(2K)/(m)}`