Question

Solve each equation for x.

a. x−10=0
b. x/2+20=0
c. Demanding Dwight insists that you give him two solutions to the following equation:
(x−10)(x/2+20)=0
Can you provide him with two solutions?

Answer 1

a) x = 10

b) x = -40

c) x = 10, -40

Explanation:

a)

`x-10=0`

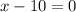
Taking 10 to the right hand side 10 becomes positive

`\\\Rightarrow x=10`

So x = 10

b)

`(x)/(2)+20=0`

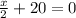
Taking 20 to the right hand side 20 becomes negative

`(x)/(2)=-20`

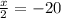
Multiplying both sides by 2

`x=-40`

So, x = -40

c)

`(x-10)((x)/(2)+20)=0\\\Rightarrow x-10=0, (x)/(2)+20=0\\\Rightarrow x=10, (x)/(2)=-20\\\Rightarrow x=10, x=-40`

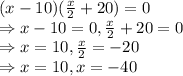
Hence, x = 10, -40

So, two solutions can be provided