Question

Rewrite
`\sqrt{n^(3)p^(4) }` as an exponential expression

Answer 1

n^3/2 p^2.

Explanation:

Note √x = x^1/2 so:

√(n^3p^4)

= (n^3)^1/2 (p^4)^1/2

= n^(3*1/2) p^4 * 1/2)

= n^3/2 p^2.

Answer 2

`{n}^{1(1)/(2)}{p}^(2)`

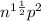
Explanation:

According to the Definition of Rational Exponents, use this formula to rewrite this as an exponential expression:

`a^{(m)/(n)} = \sqrt[n]{a}^(m)`

NOTE: Since we have exponents in our radical, we have to multiply all exponents by one-half, since raising something to its half power is the exact same as taking the square root of something:

`[{n}^(3){p}^(4)]^{(1)/(2)} = {n}^{1(1)/(2)}{p}^(2)`

* Do not forget to remove the radical in the beginning because you are once again, rewriting this as an exponential expression.

I am joyous to assist you anytime.