Answer:
I wil have traveled 20 miles by the moment I meet my friend
Explanation:
Hi
We are going to use de following formula
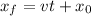
In my case speed will be positive, so
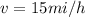 and
and
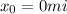 , For my friend speed will be negative, so
, For my friend speed will be negative, so
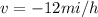 and
and
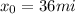 . Then we can build two equations
. Then we can build two equations
(1)

(2)
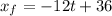
By replacing (1) in (2)
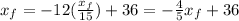
Multiplying both sides by 5
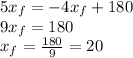
So I wil have traveled 20 miles by the moment I meet my friend.