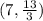Answer:
Explanation:
we have
The equation of the first line
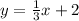 ------> equation A
------> equation A
The equation of the second line
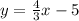 ------> equation B
------> equation B
Solve the system of equations by elimination
Multiply equation A by -4 both sides

 --------> equation C
--------> equation C
Adds equation B and equation C
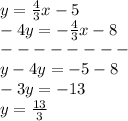
Find the value of x
substitute the value of y

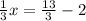
Multiply by 3 both sides
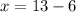
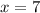
therefore
The solution to the system of equations is the point