Question

Simplify the following rational expression : ((x²y)²(xy)³z²)/((xy²)²yz).

Answer 1

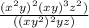`((x^2y)^2(xy)^3z^2))/(((xy^2)^2yz))` = x⁵z

Explanation:

Expression given in the question:

`((x^2y)^2(xy)^3z^2))/(((xy^2)^2yz))`

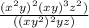
now,

when the power is applied to the number with power, the power of the number gets multiplied i.e

(Xᵃ)ᵇ = Xᵃᵇ

The number having same base when multiplied together, the powers of the numbers gets added

Xᵃ × Xᵇ = Xᵃ⁺ᵇ

and,

The number having same base are when divided , the powers of the numbers gets subtracted

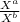`(X^a)/(X^b)` = Xᵃ⁻ᵇ

thus using the above property, we get

⇒
`\frac{(x^(2)*2}y^2)(x^3y^3)z^2)}{((x^2y^(2*2))yz)}`

or

⇒
`((x^(4)y^2)(x^3y^3)z^2))/(((x^2y^(4))yz))`

or

⇒
`((x^(4)x^3y^2y^3)z^2))/((x^2y^(4)yz))`

or

⇒
`((x^(4+3)y^(2+3))z^2))/((x^2y^(4+1)z))`

or

⇒
`((x^(7)y^(5))z^2))/((x^2y^(5)z))`

or

⇒
`(x^(7-2)y^(5-5))z^(2-1))`

or

⇒
`(x^(5)y^(0))z^(1))`

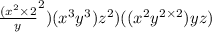
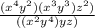
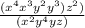
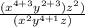
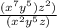
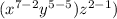
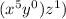
or

⇒ x⁵z