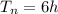Answer: 6 hours
Step-by-step explanation:
The question seems incomplete, however, it is written below:
Suppose the Earth were to suddenly shrink to half its current diameter, with its mass remaining constant, what would be the duration of the new day (in hours)?
This can be solved knowing the radius of the Earth
 is half its diameter
is half its diameter
 :
:
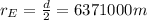
Hence, if this diameter is "suddenly shrink to half" the new radius will be also the half of
 :
:
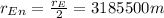
With this in mind, by the Conservation of Angular Momentum we have:
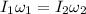 (1)
(1)
Where:
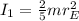 (2) is the inertia of the Earth with its current radius and
(2) is the inertia of the Earth with its current radius and
 its constant mass
its constant mass
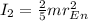 (3) is the inertia of the Earth with its new radius
(3) is the inertia of the Earth with its new radius
 (4) is the current angular velocity of the Earth with a period
(4) is the current angular velocity of the Earth with a period
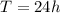
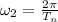 (5) is the new angular velocity of the Earth with a new period
(5) is the new angular velocity of the Earth with a new period
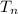
Substituting these equations in (1):
 (6)
(6)
Isolating
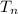 :
:
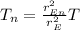 (7)
(7)
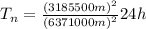
Finally: