Show that the folowing complex numbers have the same argument. a. z1 = 3 + 3√3i and z2 = 1 + √3i b. z1 = 1 + i and z2 = 4 + 4i

Question

asked Apr 23, 2020 16.9k views

1 Answer

Tmdean · Answer 1 · 2020-04-26T18:05:42+0000

Answer and explanation

(a) We have given that
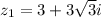
z_1=3+3√(3)i

And
z_2=1+√(3)i

We have to prove that both complex number has same argument

Argument is given by
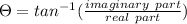
$\Theta =tan^(-1)((imaginary\ part)/(real\ part))$

Argument of
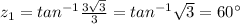
$z_1=tan^(-1)(3√(3))/(3)=tan^(-1)√(3)=60^(\circ)$

Argument of
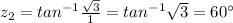
$z_2=tan^(-1)(√(3))/(1)=tan^(-1)√(3)=60^(\circ)$

Hence both
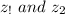$z_!\ and\ z_2$ have same argument

(b) We have given We have given that
z_1=1+i

And
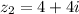
z_2=4+4i

We have to prove that both complex number has same argument

Argument is given by
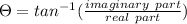
$\Theta =tan^(-1)((imaginary\ part)/(real\ part))$

Argument of
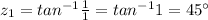
$z_1=tan^(-1)(1)/(1)=tan^(-1)1=45^(\circ)$

Argument of
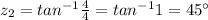
$z_2=tan^(-1)(4)/(4)=tan^(-1)1=45^(\circ)$

Hence both
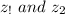$z_!\ and\ z_2$ have same argument