Question

Find the future values of these ordinary annuities. Compounding occurs once a year. Round your answers to the nearest cent.Rework previous parts assuming that they are annuities due. Round your answers to the nearest cent.$200 per year for 12 years at 10%.$100 per year for 6 years at 5%.$600 per year for 10 years at 0%.$200 per year for 12 years at 10%.$100 per year for 6 years at 5%.$600 per year for 10 years at 0%

Answer 1

a. $ 4,276.86

b. $ 680.19

c. $ 6,000

d. $ 4,704.55

e. $ 714.20

f. $ 6,000

Explanation:

The following formula applies to the first two items:

`FV=P[((1+r)^(n)-1 )/(r) ]`

Where:

P = Periodic payment.

r = rate per period.

n = number of periods.

a. $ 200 per year for 12 years at 10%.

In this case: P = $200, r = 10% or 0.1, and n = 12

We replace in the FV formula:

`FV = 200[((1+0.1)^(12)-1 )/(0.1) ]`

`FV=200[ (1.1^(12) -1)/(0.1) ]`

`FV=200[(2.138428)/(0.1) ]`

`FV=200*21.384284`

`=4,276.86`

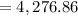
b. $100 per year for 6 years at 5%.

In this case: P = $100, r = 5% or 0.05, and n = 6.

We replace in the FV formula:

`FV = 100[((1+0.05)^(6)-1 )/(0.05) ]`

`FV=100[ (1.05^(6) -1)/(0.05) ]`

`FV=100[(0.3400956406)/(0.05) ]`

`FV=100*6.8019128`

`=680.19`

c. $600 per year for 10 years at 0%.

If the interest rate is 0%, simply multiply the amount of money by the number of years during which it will be received.

In this case: P = $600, and n = 10

`FV=600*10`

`FV=6000`

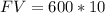
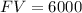
For the items d. and e., the Future Value of Annuity Due must be applied.

`FVAD=(1+r)*P[((1+r)^(n)-1 )/(r) ]`

It is the same as saying:

`FVAD=(1+r)*FV`

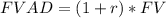
d. $200 per year for 12 years at 10%.

In this case: P = $200, r = 10% or 0.1, n = 12, and FV = 4,276.86 (We obtained this in a. ).

We replace in the FVAD formula:

`FVAD=(1+0.1)*(4,276.86)`

`FVAD=(1.1)*(4,276.86)`

`FVAD=4,704.546`

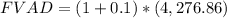
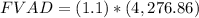
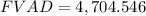
FVAD = 4,704.546 or (rounded) 4,704.55

e. $100 per year for 6 years at 5%.

In this case: P = $100, r = 5% or 0.05, n = 6, and FV = 680.2 (We obtained this in b. ).

We replace in the FVAD formula:

`FVAD=(1+0.05)*(680.19)`

`FVAD=(1.05)*(680.19)`

`FVAD=714.1995`

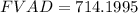
FVAD = 714.1995 or (rounded) 714.20.

f. $600 per year for 10 years at 0%

Because the interest rate is 0, the ordinary annuity is exactly the same as the due one, that is, $ 6,000.