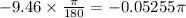Answer:
(a) In polar form complex number will be
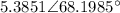 and in radian argument is 0.378π
and in radian argument is 0.378π
(b)
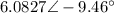
angle will be 0.05255π
Explanation:
We have given
(a) 2+5i
We have to represent in polar form
We know that magnitude is given by

Argument is given by
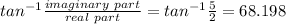
So in polar form complex number will be
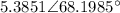
In radian argument will be
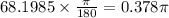
(b) We have given complex number
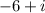
We know that magnitude is given by
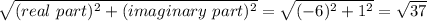
Argument is given by
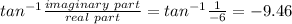
So in polar form complex number will be
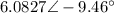
In radian argument will be