Question

Find the zeros of the following polynomial functions, with their multiplicities. (a) f(x)= (x +1)(x − 1)(x² +1) (b) g(x) = (x − 4)^3(x − 2)^8 (c) h(x) = (2x − 3)^5 (d) k(x) =(3x +4)^100(x − 17)^4

Answer 1

a) zeros of the function are x = 1 and, x = -1

b) zeros of the function are x = 2 and, x = 4

c) zeros of the function are x =
`(3)/(2)`

d) zeros of the function are x =
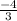`(-4)/(3)` and, x = 17

Explanation:

Zeros of the function are the values of the variable that will lead to the result of the equation being zero.

Thus,

a) f(x)= (x +1)(x − 1)(x² +1)

now,

for the (x +1)(x − 1)(x² +1) = 0

the condition that must be followed is

(x +1) = 0 ..........(1)

or

(x − 1) = 0 ..........(2)

or

(x² +1) = 0 ...........(3)

considering the equation 1, we have

(x +1) = 0

or

x = -1

for

(x − 1) = 0

x = 1

and,

for (x² +1) = 0

or

x² = -1

or

x = √(-1) (neglected as it is a imaginary root)

Thus,

zeros of the function are x = 1 and, x = -1

b) g(x) = (x − 4)³(x − 2)⁸

now,

for the (x − 4)³(x − 2)⁸ = 0

the condition that must be followed is

(x − 4)³ = 0 ..........(1)

or

(x − 2)⁸ = 0 ..........(2)

considering the equation 1, we have

(x − 4)³ = 0

or

x -4 = 0

or

x = 4

and,

for (x − 2)⁸ = 0

or

x - 2 = 0

or

x = 2

Thus,

zeros of the function are x = 2 and, x = 4

c) h(x) = (2x − 3)⁵

now,

for the (2x − 3)⁵ = 0

the condition that must be followed is

(2x − 3)⁵ = 0

or

2x - 3 = 0

or

2x = 3

or

x =
`(3)/(2)`

Thus,

zeros of the function are x =
`(3)/(2)`

d) k(x) =(3x +4)¹⁰⁰(x − 17)⁴

now,

for the (3x +4)¹⁰⁰(x − 17)⁴ = 0

the condition that must be followed is

(3x +4)¹⁰⁰ = 0 ..........(1)

or

(x − 17)⁴ = 0 ..........(2)

considering the equation 1, we have

(3x +4)¹⁰⁰ = 0

or

(3x +4) = 0

or

3x = -4

or

x =
`(-4)/(3)`

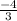
and,

for (x − 17)⁴ = 0

or

x - 17 = 0

or

x = 17

Thus,

zeros of the function are x =
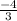`(-4)/(3)` and, x = 17