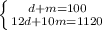Question

Michael uses a blend of dark chocolate and milk chocolate to make the ice cream topping at his restaurant. He needs to buy 100kg chocolate in total for his next order. Dark chocolate costs $12 per kilogram, milk chocolate costs $10 per kilogram, and he wants to spend $1120 total.

Answer 1

Answer:
`\left \{ {{d+m=100} \atop {12d+10m=1120}} \right.`

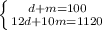
Explanation:

The complete exercise is: "Michael uses a blend of dark chocolate and milk chocolate to make the ice cream topping at his restaurant. He needs to buy 100 kg of chocolate in total for his next order. Dark chocolate costs $12 per kilogram, milk chocolate costs $10 per kilogram, and he wants to spend $1120 total. Let "d" be the number of kilograms of dark chocolate he buys and "m" be the number of kilograms of milk chocolate he buys. Which system of equations represents this situation?"

Let be "d" the number of kilograms of dark chocolate MIchael buys and "m" the number of kilograms of milk chocolate he buys.

Since Michaels needs to buy a total of 100 kilogram of chocolate, we know that the sum of "d" and "m" is 100. Knowing this, we can write this equation:

`d+m=100`

Knowing that the Dark chocolate costs $12 per kilogram (which can be expressed with
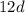`12d`) and milk chocolate costs $10 per kilogram (this can be expressed
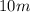`10m`), and he wants to spend $1120 total, we can write the following equation to represent this:

`12d+10m=1120`

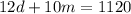
Therefore, the system of equations that represents this situation is:

`\left \{ {{d+m=100} \atop {12d+10m=1120}} \right.`