Answer:
See the explanation.
Explanation:
If a triangle is a right triangle, then it should follow pythagoras theorem.
So sum of squares of two sides is equal to the square of the third longest side.

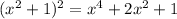
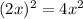
Adding the first and third equation we get the second equation.
So it follows Pythagoras theorem.
Hence it is a right triangle with
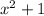 as the hypotenuse.
as the hypotenuse.