Question

Given z1 = 1+i and z2 = 2+3i.

a. Let w = z1 ⋅ z2. Find w and the multiplicative inverse of w.
b. Show that the multiplicative inverse of w is the same as the product of the multiplicative inverses of z1 and z2.

Answer 1

(a)
`w=2+5i-6=-4+5i`

Multiplicative inverse of w will be
`(1)/(-4+5i)`

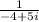
(B) As w is same as the product of
`z_1\ and\ z_2`

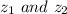
So there multiplicative inverse will also be same

Explanation:

We have given two complex numbers

`z_1=1+i` and
`z_2=3+2i`

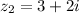
(a) First we have to find
`w=z_1z_2`

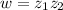
So
`w=(1+i)(2+3i)=2+3i+2i+6i^2=2+5i+6i^2`

As we know that
`i^2=-1`

So
`w=2+5i-6=-4+5i`

Multiplicative inverse :

It is that number when multiply with the number which we have have to find the multiplicative inverse gives result as 1

So multiplicative inverse of w will be
`(1)/(-4+5i)`

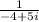
Because when we multiply
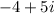`-4+5i` with
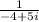`(1)/(-4+5i)` it gives result as 1

(b) As w is same as the product of
`z_1\ and\ z_2`

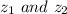
So there multiplicative inverse will also be same