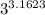Question

. Use the process outlined in the lesson to approximate the number 3√10. Use the approximation √10 ≈3162 277 7.

. Find a sequence of five intervals that contain 3√10 whose endpoints get successively closer to 3√10. Write your
iintervals in the form 3^???? < 3^√10 < 3^s for rational numbers ????and s.

Answer 1

sequence of five intervals

(1) 3³ <
`3^(√(10) )` <
`3^(4)`

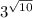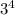
(2)
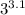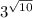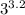
`3^(3.1)` <
`3^(√(10) )` <
`3^(3.2)`

(3)
`3^(3.16)` <
`3^(√(10) )` <
`3^(3.17)`

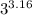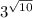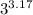
(4)
`3^(3.162)` <
`3^(√(10) )` <
`3^(3.163)`

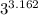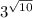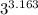
(5)
`3^(3.1622)` <
`3^(√(10) )` <
`3^(3.1623)`

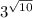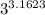
Explanation:

as per question given data

√10 ≈ 3.162 277 7

to find out

sequence of five intervals

solution

as we have given that √10 value that is here

√10 ≈ 3.162 277 7 ........................1

so

when we find
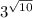`3^(√(10) )` ................2

put here √10 value in equation number 2

we get
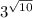`3^(√(10) )` that is 32.27

so

sequence of five intervals

(1) 3³ <
`3^(√(10) )` <
`3^(4)`

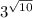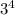
(2)
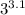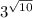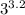
`3^(3.1)` <
`3^(√(10) )` <
`3^(3.2)`

(3)
`3^(3.16)` <
`3^(√(10) )` <
`3^(3.17)`

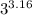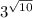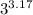
(4)
`3^(3.162)` <
`3^(√(10) )` <
`3^(3.163)`

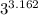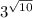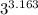
(5)
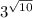`3^(3.1622)` <
`3^(√(10) )` <
`3^(3.1623)`