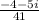Answer:
(a)
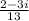
(b)
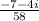
(c)
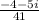
Explanation:
We have the expressions an we have to find the multiplicative inverse
Multiplicative inverse
Multiplicative inverse is that number which when multiply with the number for which we have to find the multiplicative inverse gives result as 1
(a)
 its multiplicative inverse will be
its multiplicative inverse will be
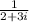
After rationalizing
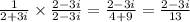 So multiplicative inverse will be
So multiplicative inverse will be
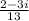
(b) We have given number

Multiplicative inverse will be
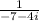
After rationalizing
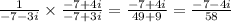
(c) We have given number
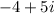
Its multiplicative inverse will be
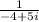
After rationalizing
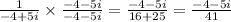
So its multiplicative inverse will be