Question

Find the quotient (a) x^n-1 ÷ x-1 for n = 2, 3, 4, and 8 (b) What patterns do you notice? (c) Use your work in part (a) to write an expression equivalent to x^n-1 ÷ x-1 for any integer n > 1.

Answer 1

(a)
`(x^(2) -1)/(x-1) =1+x`

`(x^(3) -1)/(x-1) =1+x+x^(2)`

`(x^(4)-1 )/(x-1) =x^(3)+x^(2)  +x+1`

`(x^(8)-1 )/(x-1) =x^(7)+x^(6)+x^(5)+x^(4)+x^(3)+x^(2)+1`

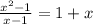
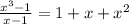
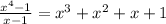
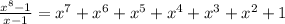
(b) when we divide (
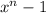`x^(n) -1`) with (x-+1) then the quotient will be a polynomial of x with (n-1) degree and all the coefficients are 1.

(c)
`[1+x^(2) +x^(3)+x^(4)+x^(5)+.....+x^(n-2) +x^(n-1) ]`

Explanation:

(a) We have,
`(x^(2) -1)/(x-1) =((x-1)(x+1))/(x-1) =1+x` (Answer)

and,
`(x^(3) -1)/(x-1) =((x-1)(x^(2)+x+1) )/(x-1)=1+x+x^(2)` (Answer)

and,
`(x^(4)-1 )/(x-1) =((x-1)(x+1)(x^(2)+1) )/(x-1)=(x+1)(x^(2)  +1) =x^(3)+x^(2)  +x+1` (Answer)

and,
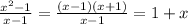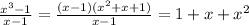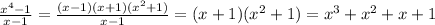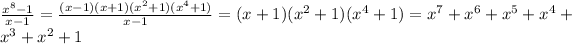`(x^(8)-1 )/(x-1) = ((x-1)(x+1)(x^(2)+1)(x^(4) +1) )/(x-1) =(x+1)(x^(2)+1)(x^(4) +1) =x^(7)+x^(6)+x^(5)+x^(4)+x^(3)+x^(2)+1` (Answer)

(b) From the above four quotients it is clear that when we divide (
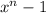`x^(n) -1`) with (x-+1) then the quotient will be a polynomial of x with (n-1) degree and all the coefficients are 1. (Answer)

(c) Hence, from the above pattern of the quotients we can write the expression which is equivalent to
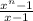`(x^(n)-1 )/(x-1)` will be

`[1+x^(2) +x^(3)+x^(4)+x^(5)+.....+x^(n-2) +x^(n-1) ]` (Answer)