Question

Determine algebraically wheather or not the function f(x)=-x^3 -2x^2 +5 is even or odd and justify your answer

Answer 1

The function f(x) is neither even, nor odd function.

Explanation:

Definition: A function is called an even function if for all x from its domain

`f(-x)=f(x)`

Definition: A function is called an odd function if for all x from its domain

`f(-x)=-f(x)`

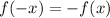
You are given the function
`f(x)=-x^3-2x^2+5.`

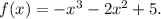
Substitute into the function expression -x instead of x.

`f(-x)=-(-x)^3-2(-x)^2+5\\ \\f(-x)=-(-x^3)-2x^2+5=x^3-2x^2+5\\eq f(x)\\ \\-f(x)=-(-x^3-2x^2+5)=x^3+2x^2-5\\ \\f(-x)\\eq -f(x)`

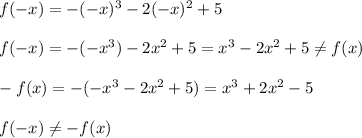
Hence, the function f(x) is neither even, nor odd function.