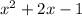Answer:
So in standard form equation will be
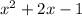
Explanation:
We have given expression
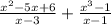
Let first we solve first part of the expression
So
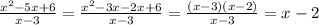
Now second part
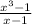
We know the algebraic identity
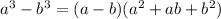
So by using this identity
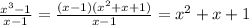
Now adding first and second part
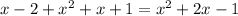
So in standard form equation will be