Question

3. A football is kicked with a speed of 35 m/s at an angle of 40°.

a. What is the initial vertical velocity?
b. What is the initial horizontal velocity?
C. How much time does it take to reach maximum height?
d. What is the maximum height?
e. How far down the field does it land?

Answer 1

a) 22.5 m/s

The initial vertical velocity is given by:

`u_y = u sin \theta`

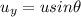
where

u = 35 m/s is the initial speed

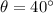`\theta=40^(\circ)` is the angle of projection of the ball

Substituting into the equation, we find

`u_y = (35)(sin 40)=22.5 m/s`

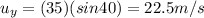
b) 26.8 m/s

The initial horizontal velocity is given by:

`u_x = u cos \theta`

where

u = 35 m/s is the initial speed

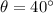`\theta=40^(\circ)` is the angle of projection of the ball

Substituting into the equation, we find

`u_x = (35)(cos 40)=26.8 m/s`

c) 2.30 s

The time it takes for the ball to reach the maximum heigth can be found by considering the vertical motion only. This is a uniformly accelerated motion (free-fall), so we can use the suvat equation

`v_y = u_y + at`

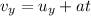
where

`v_y` is the vertical velocity at time t

`u_y = 22.5 m/s`

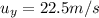
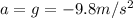`a=g=-9.8 m/s^2` is the acceleration of gravity (negative because it is downward)

At the maximum height, the vertical velocity becomes zero,
`v_y =0`; substituting, we find the time t at which this happens:

`0=u_y + gt\\t=-(u_y)/(g)=-(22.5)/(-9.8)=2.30 s`

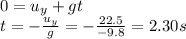
d) 25.8 m

The maximum height can also be found by considering the vertical motion only. We can use the following suvat equation:

`s=u_y t + (1)/(2)gt^2`

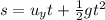
where

s is the vertical displacement at time t

`u_y = 22.5 m/s`

`g=-9.8 m/s^2`

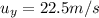
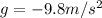
Substituting t = 2.30 s, we find the displacement at maximum height, so the maximum height:

`s=(22.5)(2.30)+(1)/(2)(-9.8)(2.30)^2=25.8 m`

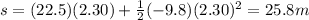
e) 123.3 m

In order to find how far does the ball lands, we have to consider the horizontal motion.

First of all, the time it takes for the ball to go back to the ground is twice the time needed for reaching the maximum height:

`t=2(2.30 s)=4.60 s`

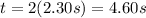
Then, we consider the horizontal motion. There is no acceleration along this direction, so the horizontal velocity is constant:

`v_x = 26.8 m/s`

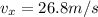
Therefore, the horizontal distance travelled during the whole motion is

`d=v_x t = (26.8)(4.60)=123.3 m`

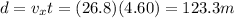
So, the ball lands 123.3 m far from the initial point.