Question

A body falls from the top of the tower and during the last second of its fall it fall through 23mvfind height of tower.

​

Answer 1

39.7 m

Step-by-step explanation:

First, we conside only the last second of fall of the body. We can apply the following suvat equation:

`s=ut+(1)/(2)at^2`

where, taking downward as positive direction:

s = 23 m is the displacement of the body

t = 1 s is the time interval considered

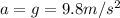`a=g=9.8 m/s^2` is the acceleration

u is the velocity of the body at the beginning of that second

Solving for u, we find:

`ut=s-(1)/(2)at^2\\u=(s)/(t)-(1)/(2)at=(23)/(1)-(1)/(2)(9.8)(1)=18.1 m/s`

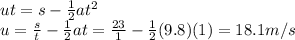
Now we can call this velocity that we found v,

v = 18 m/s

And we can now consider the first part of the fall, where we can apply the following suvat equation:

`v^2-u^2 = 2as'`

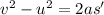
where

v = 18 m/s

u = 0 (the body falls from rest)

s' is the displacement of the body before the last second

Solving for s',

`s'=(v^2-u^2)/(2a)=(18.1^2-0)/(2(9.8))=16.7 m`

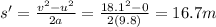
Therefore, the total heigth of the building is the sum of s and s':

h = s + s' = 23 m + 16.7 m = 39.7 m