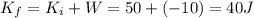Question

The force experienced by a 0.250 kg particle is depicted in the figure below. The particle

approaches the origin from the right at a speed of 20.0 m/s. (a) Find the work done by the force as
the particle moves from x=6.00 m to x = 0. (b) What is the kinetic energy of the particle at the
origin?
2

Answer 1

(a) -10 J

The graph represents the force versus the position of the particle: this means that the area under the graph represent the work done on the particle.

Therefore, let's start by calculating the area. The area of the trapezium between x = 0 and x = 3 m is:

`A_1 = (1)/(2)(3+2)\cdot (-10)=-25`

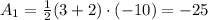
While the area of the triangle between x = 3 m and x = 6 m is

`A_2 = (1)/(2)(3\cdot 10)=15`

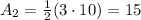
So, the work done on the particle is

`W=A_1 + A_2 = -25 +15 = -10 J`

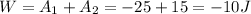
(b) 40 J

The kinetic energy of the particle is given by

`K=(1)/(2)mv^2`

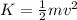
where

m is its mass

v is its speed

The mass of the particle is

m = 0.250 kg

While the initial speed is

v = 20.0 m/s

So the initial kinetic energy (at x = 6 m) is

`K_i = (1)/(2)(0.250)(20)^2=50 J`

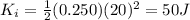
For the work-energy theorem, the final kinetic energy of the particle (at x=0) will be the initial kinetic energy + the work done by the force on it, therefore:

`K_f = K_i + W = 50 + (-10) = 40 J`