Question

An experienced window washer can wash all the windows in Mike’s house in 2 hours, while a new trainee can wash all the windows in 7 hours. How long would it take them working together? Round your answer to the nearest minute if needed.

Answer 1

The experienced window washer can wash all the windows in Mike’s house in 2 hours, which implies that in 1 hour he completes 1/2 of the job.

By the same logic, the new trainee completes 1/7 of the job in one hour.

If they work together, they complete

`(1)/(2)+(1)/(7)=(7)/(14)+(2)/(14)=(9)/(14)`

of the job in one hour, meaning that they complete the job in 14/9 of a hour.

Answer 2

It would take 1.55 hours or 93.6 minutes for them if they work together.

Solution:

Let us assume together both can complete the work in x hours.

Experienced window washer can wash the house in 2 hours.

So, in 1 hour he will do,
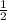`(1)/(2)` part of the house

Hence, in x hours he will do
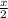`(x)/(2)` part of the house

Again the trainee can wash all the windows in 7 hours

So, in 1 hour he will do,
`(1)/(7)` part of the house

Hence, in x hours he will do
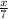`(x)/(7)` part of the house

We can now say,

`\Rightarrow (x)/(2)+(x)/(7)=1`

`\Rightarrow \quad x *\left((7+2)/(14)\right)=1 \\\\ \Rightarrow x *\left((9)/(14)\right)=1 \\\\ \Rightarrow x=(14)/(9)=1.55`

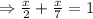
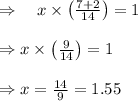
They can complete in 1.55 hours.

1 hour = 60 minutes

So, according to unitary method,
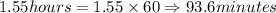`1.55 hours = 1.55*60 \Rightarrow 93.6 minutes`.