Answer:
Option C. The given system has two solutions.
Solution:
The given equations are,
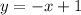
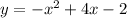
From the equation we can say,

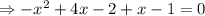

We know that the quadratic formula to solve this,
x has two values which are

Here, a = (-1), b = 5 , c = -3
So,
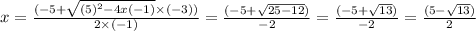
Again
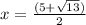
Hence, x has two solutions.