Question

Let AB be the directed line segment beginning at point A(3 , 2) and ending at point B(-12 , 10). Find the point P on the line segment that partitions the line segment into the segments AP and PB at a ratio of 4:5

Answer 1

The coordinates of point P are:

`\displaystyle \left(-(11)/(3), (50)/(9)\right)`.

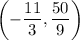Explanation:

`\rm |AB| = |AP| + |PB|`.

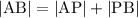Therefore, if

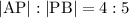`\rm |AP|:|PB| = 4 :5`, then

`\rm |PB| : |AB| = |PB| : (|AP| + |PB|) = 5: (4 + 5) = 5 : 9`.

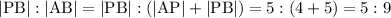Consider: what's the horizontal and vertical separation between point A and point B?

Horizontal Separation

Note that the
`x`-coordinate (the first of the two) of point B is smaller than that of point A by
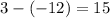`3 - (-12) = 15`. In other words, point A is to the right of point B with a horizontal separation of
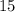`15` units.

However, since point P is somewhere between point A and B, it should also also be to the left of point B. Additionally, since
`\rm |PB|: |AB| = 5 : 9`, point P should be to the left of point B with a horizontal separation of
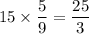`\displaystyle 15 * (5)/(9) = (25)/(3)` units.

As a result, the horizontal coordinate of point P would be
`\displaystyle \displaystyle -12 + (25)/(3) = - (11)/(3)`.

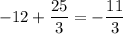Vertical Separation

Since the
`y`-coordinate (the second of the two) of point B is larger than that of point A by
`10 - 2` units, point B is above point A with a vertical separation of
`8` units.

Since point P is between point A and B, it should also be above point A and below point B. P should be below point B with a vertical separation of
`\displaystyle 8 * (5)/(9) = (40)/(9)`.

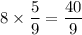As a result, the vertical coordinate of point P would be equal to
`\displaystyle 10 - (40)/(9) = (50)/(9)`.

Overall, the coordinates of point P should be
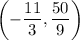`\displaystyle \left(-(11)/(3), (50)/(9)\right)`.