Question

If the length of a diagonal of a rectangle is twice the length of one of the sides of this rectangle, then what are the angle measurements between the diagonals?

Answer 1

The angle measurements between the diagonals are 60° and 120°

Explanation:

Let

D -----> the diagonal of rectangle

x -----> the length of rectangle

y ----> the width of rectangle

we know that

Applying the Pythagoras Theorem

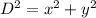`D^2=x^2+y^2` -----> equation A

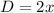`D=2x` ----> equation B

substitute equation B in equation A

`(2x)^2=x^2+y^2`

`4x^2=x^2+y^2`

`y^2=3x^2`

`y=x√(3)`

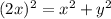
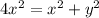
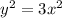
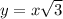
see the attached figure to better understand the problem

The triangle DOC is an isosceles triangle

m∠ODC= m∠OCD

Find the measure of angle m∠ODC

tan(∠ODC)=y/x

Remember that

`y=x√(3)`

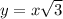
substitute

tan(m∠ODC)=x√3/x

tan(m∠ODC)=√3

m∠ODC=arc tan(√3)

m∠ODC=60°

m∠OCD=60°

Find the measure of angle m∠DOC

Remember that the sum of the internal angles of triangle must be equal to 180 degrees

The triangle DOC is an isosceles triangle

m∠ODC= m∠OCD

so

m∠ODC+ m∠OCD+m∠DOC=180°

substitute the given values

60°+ 60°+m∠DOC=180°

120°+m∠DOC=180°

m∠DOC=180°-120°=60°

Remember that the angle measurements between the diagonals are

m∠DOC and m∠BOC

The sum of the angle measurements between the diagonals is equal to 180 degrees, because are supplementary angles (form a linear pair)

we have

m∠DOC=60°

so

m∠BOC=120°

therefore

The angle measurements between the diagonals are 60° and 120°