Question

Given triangle QRP find the value of x and the measures of angles Q and R

Answer 1

m<R= 52°

m<Q= 102°

Explanation:

Since the sum of angles in a triangle = 180°,

3x+24+2x+x=180

6x+24=180

6x=180-24

6x=156

x=26

Answer 2

The value of x is 26.

Angle Q is 102° and angle R is 52°.

Explanation:

Given : Triangle QRP with
`\angle Q=(3x+24)^\circ,\ \angle R=(2x)^\circ,\ \angle P=x^\circ`

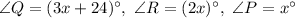
To find : The value of x and the measures of angles Q and R ?

Solution :

According to property of triangle,

Sum of all angles of a triangle is 180°.

i.e.
`\angle Q+\angle R+\angle P=180^\circ`

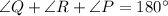
Substitute the angles,

`(3x+24)^\circ+ (2x)^\circ+x^\circ=180^\circ`

`3x+24+2x+x=180`

`6x=180-24`

`6x=156`

`x=(156)/(6)`

`x=26`

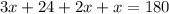
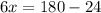
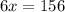
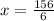
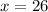
The value of x is 26.

So,
`\angle Q=(3x+24)^\circ=3(26)+24=102^\circ`

`\angle R=(2x)^\circ =2(26)=52^\circ`

`\angle P=x^\circ =26^\circ`

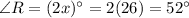
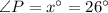
Therefore, angle Q is 102° and angle R is 52°.