Answer:
The value of x is 26.
Angle Q is 102° and angle R is 52°.
Explanation:
Given : Triangle QRP with
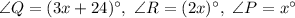
To find : The value of x and the measures of angles Q and R ?
Solution :
According to property of triangle,
Sum of all angles of a triangle is 180°.
i.e.
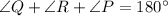
Substitute the angles,
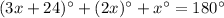
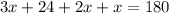
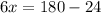
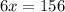
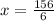
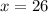
The value of x is 26.
So,
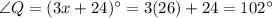
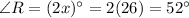
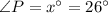
Therefore, angle Q is 102° and angle R is 52°.