Answer:
Here's how I would do it.
Explanation:
A compound inequality contains two or more inequalities that are separated by "and" or "or".
Examples are "3x - 1 <8 or x - 5 ≥ 0" and "-10 < 2 + x ≤ -1". The second example is an "and" inequality.
Let's solve the second example.
1. Solve each inequality separately
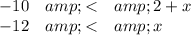
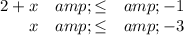
You can write the answer as "-12 < x and x ≤ -3" or "-12 < x ≤ -3" or (-12, -3]."
2. Check your solution.
Pick a point between -3 and -12 and see if it satisfies both inequalities, say, -10
-10 < 2 -10 2 + (-10) ≤ -1
-10 < -8 2 - 10 ≤ -1
-10 ≤ -1
The point satisfies both inequalities.
3. Graph the compound inequality
You can plot the graphs on a number line.
The graph of the first inequality is represented by the blue line in the first diagram below.
It starts at -3 and extends to the left. The solid circle indicates that -3 is part of the solution set.
The graph of the second inequality is represented by the red line in the second diagram.
It starts at -12 and extends to the right. The open circle indicates that -12 is not part of the solution set.
The solution to the compound inequality is the region in which the two graphs overlap — that is, from -3 down to but not including -12.
The graph is shown in the third diagram.