Question

a model rocket flies horizontally off the edge of a cliff at a velocity of 40.0m/s. if the canyon below is 110.0m deep, how far from the edge of the cliff does the model rocket land?

Answer 1

189.6 m

Step-by-step explanation:

First of all, we study the vertical motion of the rocket in order to find the time it takes for it to land. The suvat equation for the vertical motion is

`s=ut+(1)/(2)gt^2`

where, taking downward as positive direction:

s = 110.0 m is the vertical displacement

u = 0 is the initial vertical velocity

g = 9.8 m/s^2 is the acceleration of gravity

t is the time of flight

Solving for t,

`t=\sqrt{(2s)/(g)}=\sqrt{(2(110))/(9.8)}=4.74 s`

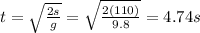
Now we can just analyze the horizontal motion, which is a uniform motion with constant velocity, which is equal to

`v_x = 40.0 m/s`

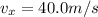
So the distance travelled horizontall after a time t is

`d=v_x t`

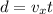
So, when the rocket lands (t = 4.74 s), the horizontal distance travelled is

`d=(40.0)(4.74)=189.6 m`

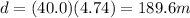
Therefore, the rocket lands 189.6 m far from the edge of the cliff.