Answer: Width= 10 yards
Length = 14 yards
Explanation:
Given : A rectangular lawn has an area of 140 square yards. It’s length is six less than twice the width.
Let x denotes the width of the rectangle .
Then, length = 2x-6
Formula : Area of rectangle = length x width
By considering the given question , we have
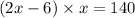
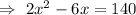
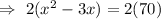
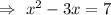
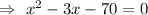
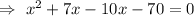
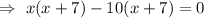
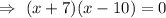
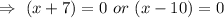
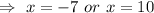
But width cannot be negative.
⇒ Width = x = 10 yards
⇒ Length = 2x-6 = 2(10)-6= 20-6 = 14 yards
Hence, the width and length of the lawn are 10 yards and 14 yards.